KMP算法

一、适用范围

一般用于字符的模式匹配问题

二、核心原理

2.1前缀函数

定义:对于长度为m的字符串s，其前缀函数为π(i)(0≤i<m)表示s的字串s[0:i]的最长的相等的
真前缀和真后缀的长度。特别地，如果不存在符合条件的前后缀，那么π(i)=0。
其中真前缀与真后缀的定义为不等于自身的前缀和后缀(就是不取下标为i的元素)。

image-20211222131049003

2.2如何求前缀函数

三、参考链接

实现 strStr() - 实现 strStr() - 力扣（LeetCode） (leetcode-cn.com)

四、next代码实现

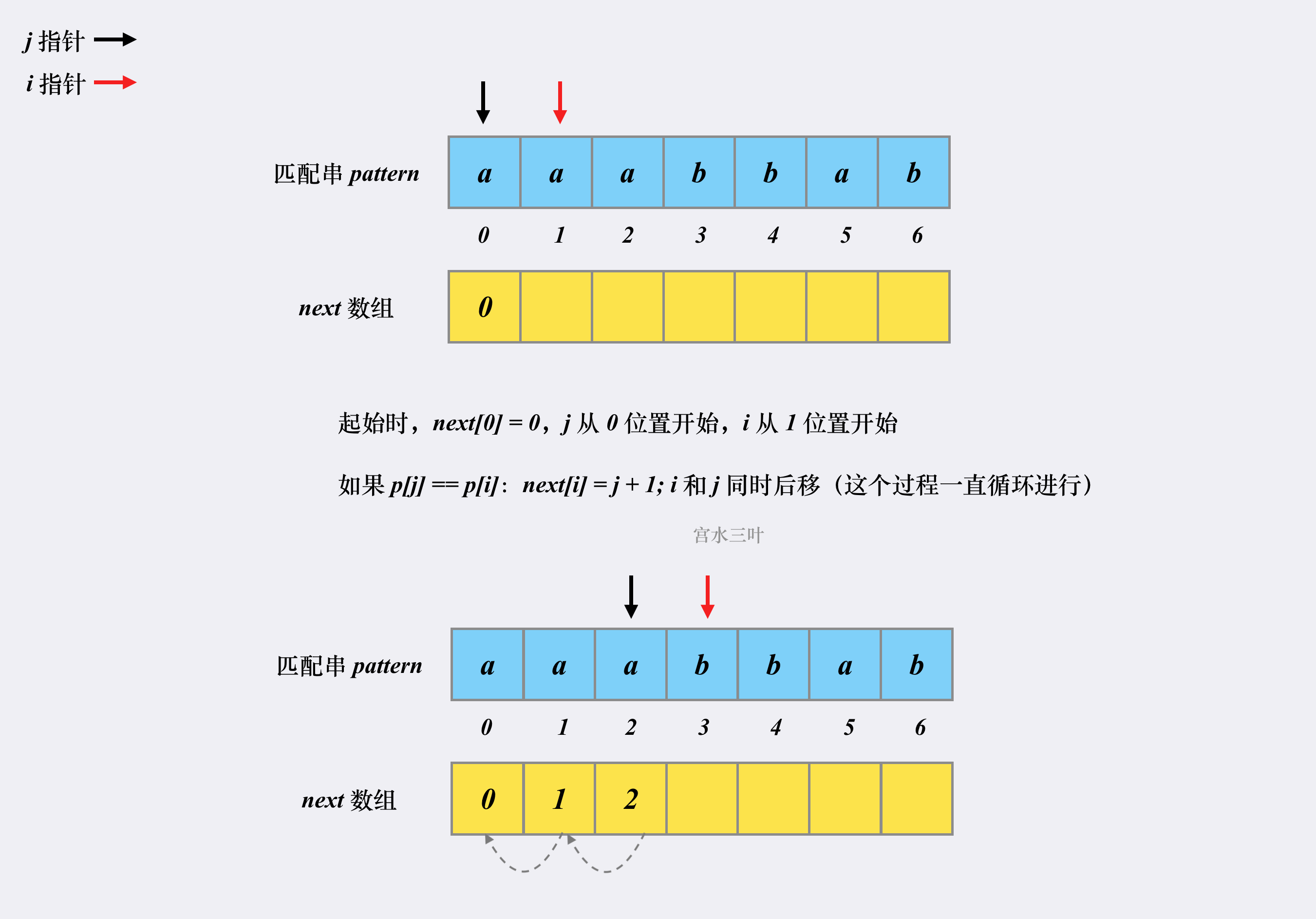
010FD8AE2B79FFE03DC3735ACD224A6A.png

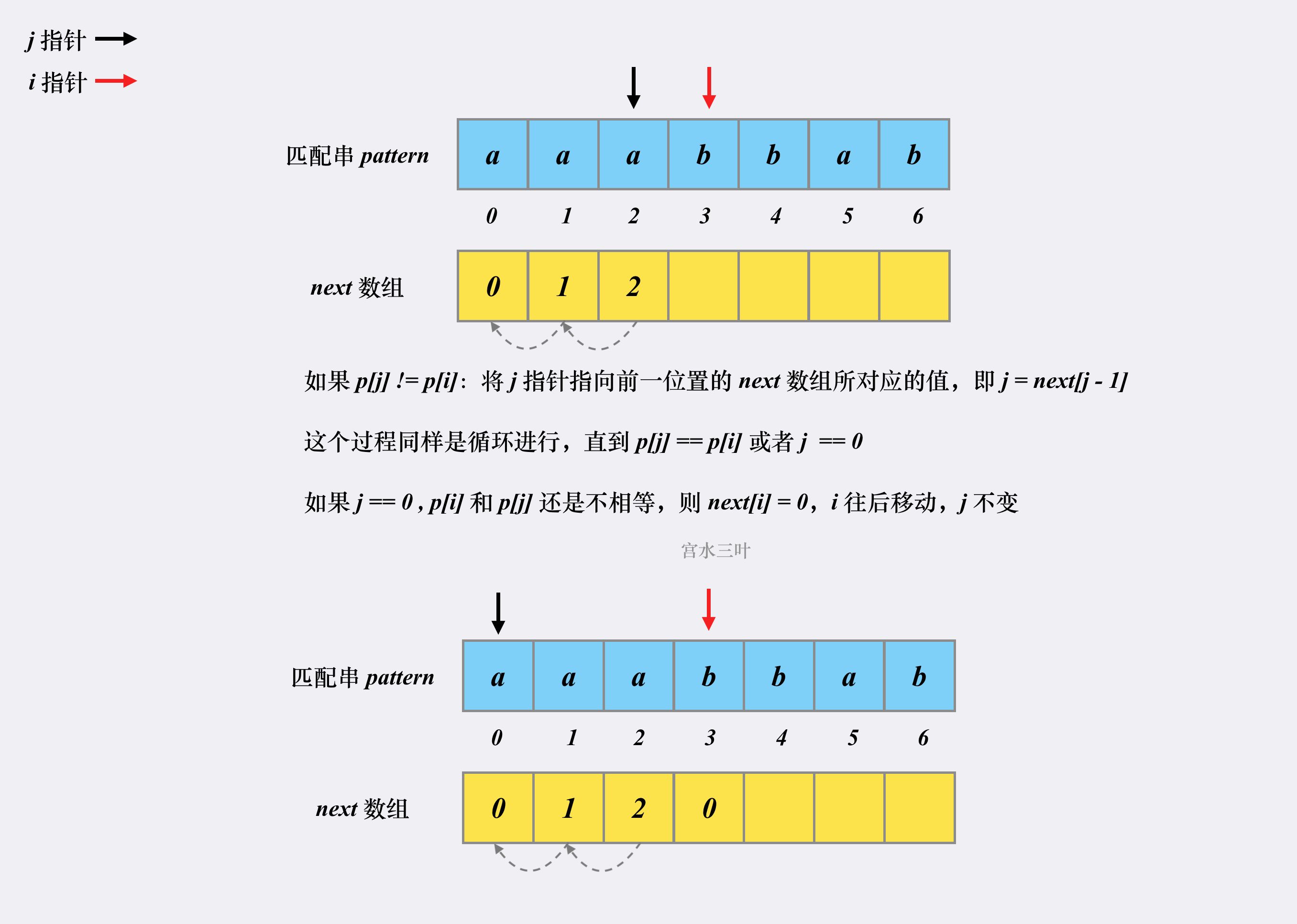
B9497542844478144BED83E9ADA0C12F.png

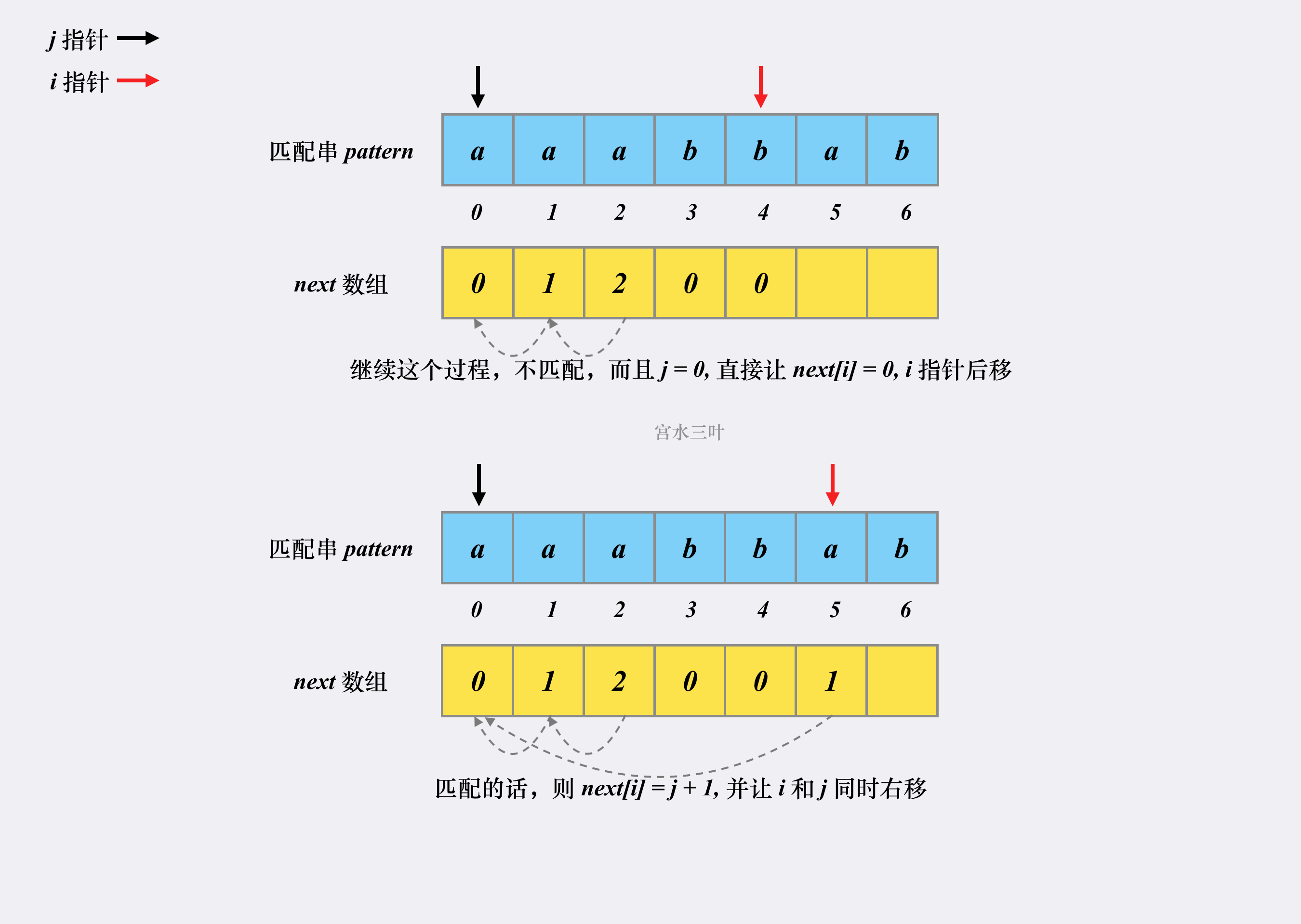
161584A2D930A7B91092A2C3872D9DE5.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int strStr(string s, string p) {
        int n = s.size(), m = p.size();
        if(m == 0) return 0;
        //设置哨兵
        s.insert(s.begin(),' ');
        p.insert(p.begin(),' ');
        vector<int> next(m + 1);//next数组
        //预处理next数组
        //i表示当前到第i个位置时，计算next[i] 和 [...i]后缀数组的包括了当前的i
        //j表示当前匹配的最长的前缀字符串的最后一个位置，
        //"aaabbbab"
        for(int i = 2, j = 0; i <= m; i++){
            while(j and p[i] != p[j + 1]) j = next[j];
            if(p[i] == p[j + 1]) j++;
            next[i] = j;
            /*
            if(p[i] == p[j + 1]){next[i] = j + 1; j++;}
            else{next[i] = 0;}
            */
            
        }
        //匹配过程
        for(int i = 1, j = 0; i <= n; i++){
            while(j and s[i] != p[j + 1]) j = next[j];
            if(s[i] == p[j + 1]) j++;
            if(j == m) return i - m;
        }
        return -1;
    }
};