基环树

一、定义

具有N个点N条边的连通图

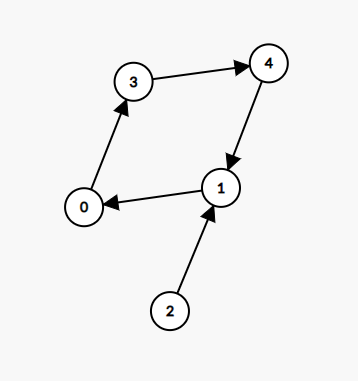
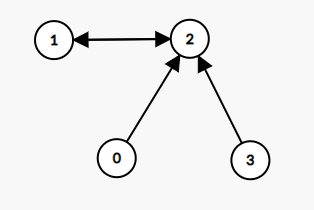
形如基环个数为>2 基环个数为=2

二、例题

力扣5970](https://leetcode-cn.com/problems/maximum-employees-to-be-invited-to-a-meeting/)

三、解题思路

由题目可知，判断一个员工是否能上桌，需要他喜欢的员工也要上桌，同时每个人身边最多只能做两个人，因此对于最后上桌的情况分为两种:

· 每个人，左边坐着喜欢自己的员工，右边做着自己喜欢的员工

· 有两个员工相互喜欢，可以补充喜欢这两个员工的人，补充的人最后一个人为没有人喜欢，
即左右两边其中一个坐着自己的喜欢的员工，另一个位置的人与自己无关。也满足题意

四、解题代码

拓扑排序 + 深度优先搜索 + 分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution {
public:
    int maximumInvitations(vector<int>& favorite) {
        int n = favorite.size();
        vector<vector<int>>g(n),rg(n);
        vector<int>degree(n);
        for(int v = 0; v < n; ++v){
            int w = favorite[v];
            g[v].emplace_back(w);
            rg[w].emplace_back(v);
            ++degree[w];//最喜欢的员工是w的人数
        }
        //拓扑排序
        queue<int>Q;
        for(int i = 0; i < n; ++i){
            if(degree[i] == 0)
                Q.push(i);
        }
        while(!Q.empty()){
            int v = Q.front();
            Q.pop();
            for(int w : g[v]){
                if (--degree[w] == 0)
                    Q.push(w);
            }
        }
        //寻找图g上的基环
        vector<int>ring;
        vector<int>vis(n);
        function<void(int)> dfs = [&](int v){
            vis[v] = true;
            ring.push_back(v);
            for(int w : g[v]){
                if(!vis[w])
                    dfs(w);
            }
        };
        //通过反向图rg寻找树枝上最深的链
        //当且仅当基环树只有两个节点时才会用到
        int max_depth = 0;
        function<void(int,int,int)>rdfs = [&](int v ,int fa ,int depth){
            max_depth = max(max_depth , depth);
            for(int w : rg[v]){
                if (w != fa){
                    rdfs(w,v,depth+1);
                }
            }
        }; 
        int max_ring_size = 0, sum_list_size = 0;
        for(int i = 0; i < n; ++i){
            if (!vis[i] && degree[i] == 1){//不是基环上的点的入度都变成了0
                ring.resize(0);
                dfs(i);
                int sz = ring.size();
                if (sz == 2){
                    int v = ring[0], w = ring[1];
                    max_depth = 0;
                    rdfs(v,w,1);
                    sum_list_size += max_depth;
                    max_depth = 0;
                    rdfs(w,v,1);
                    sum_list_size += max_depth;
                }
                else{
                    max_ring_size = max(max_ring_size , sz);
                }
            }
        }
        return max(max_ring_size,sum_list_size);
    }
};

拓扑排序 + 深度优先搜索 + 动态规划 + 分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    int maximumInvitations(vector<int>& favorite) {
        int n = favorite.size();
        int ans1 ,ans2 ; // ans1 为第一种情况只有基环 , 第二种情况为基环树
        vector<int> vis(n), degree(n),dp(n,1);
        for(int i = 0; i < n; ++i)if (not vis[i]){
            vector<int> w; 
            int x = i;
            while(not vis[x]){//精致的深度优先搜索
                w.push_back(x);
                vis[x] = 1;
                x = favorite[x];
            }
            for(int j = 0; j < w.size(); ++j){
                if (w[j] == x){
                    ans1 = max((int)w.size() - j, ans1);//进入环的位置，而末尾则为环的出口
                }
            
            }
        }
        queue<int>Q;
        for(int i = 0; i < n; ++i) degree[favorite[i]]++;
        for(int i = 0; i < n; ++i) if (degree[i] == 0){
            Q.push(i);
        }
        while(!Q.empty()){
            int u = Q.front();
            int v = favorite[u];
            Q.pop();
            dp[v] = max(dp[v],dp[u] + 1);
            if (not --degree[v]) Q.push(v);
        }
        for(int i = 0;  i < n; ++i) if (favorite[favorite[i]]== i and favorite[i] > i){//防止重复
            ans2 += dp[i] + dp[favorite[i]];
        }
        return max(ans1,ans2);
    }
};